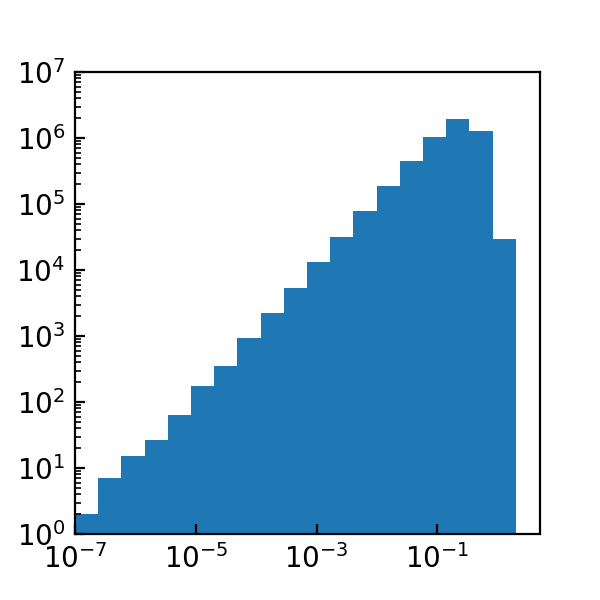
随机变量柱状图之log-log plot
对于分布函数为\(p(x)\)的随机变量,其对数\(\ln\! x\equiv y\)的分布函数为\(g(y) = e^y p(e^y)\)。也就是说,在对\(y\)的样本做柱状图时,\(\Delta\! N = e^y p(e^y) \Delta\! y\),于是有\[\ln\! \Delta\! N = y + \ln p(e^y) + \ln\! \Delta\! y.\]
如果只关注\(y\)取负值的区域,则\(e^y=x\)是接近于零的正数,并且只在很小的范围内变动。如果\(p(x)\)在\(x\)接近零的时候存在非零极限,则当\(y\)取不同的负值的时候,\(p(e^y)\)变化很小。
于是\(\ln\! \Delta\! N\)与\(y\)近似呈线性关系。比如,如果\(x\)满足正态分布,则\(x\)的柱状图的log-log plot (柱状图格子间隔在对数坐标下是等间隔的) 的左侧就会表现为相当完美的线性形态。
下面是一个数值实验。
z = np.random.normal(loc=0, scale=0.3, size=10000000)
fig = plt.figure(figsize=(3,3))
ax = fig.add_subplot(1,1,1)
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlim((1e-7,5))
ax.set_ylim((1e0,1e7))
_ = ax.hist(z.flatten(), bins=np.logspace(-7,0.3, num=20))