平稳性的定义

来源：R.S. Tsay, Analysis of Financial Time Series

严格平稳性: 任意多个点的联合分布具有时间平移不变性。

弱平稳性: 每个点的期望值以及相同距离两点之间的协方差不随时间变化。这意味着：a. 期望值是常数，即 \(E(r_t) = \mu\)；b. 任意两点之间的协方差只与这两点之间的距离有关，即 \(\text{Cov}(r_t, r_{t-l}) = \gamma_l\)。从直觉上理解，满足弱平稳性的时间序列应该围绕相同的期望值做幅度不变的振荡。

严格平稳性不一定意味着弱平稳性，因为即便联合分布具有时间平移不变性，有可能均值和协方差根本不存在 (为无穷大)。当然，如果均值和协方差都存在，则严格平稳性意味着弱平稳性。从弱平稳性一般推不出严格平稳性，但对于服从正态分布的时间序列，两者是等价的。

金融文献中通常假定资产收益率是弱平稳的。如果有足够多的历史数据，则可以检验这个假设。比如，可以把数据分割称子样本，然后看不同子样本得出的统计量是否一致。

然后这本书就没怎么提如何检验时间序列的平稳性了。

平稳性的检验

来源： Tests of Stationarity

参考的这个网页还提到一种更弱的平稳性，被称为一阶平稳，即只要求期望值平稳。还提到经济学家对这类更弱的时间序列很感兴趣，特别是怎么把均值随时间变化的时间序列组合成一个一阶平稳的时间序列 (不太明白是在做什么，我猜可能是把时间序列分段上下平移并对齐，天文领域经常需要对光谱做这类事。)。

然后作者 (Guy Nason, 布里斯托大学统计学教授) 提到了一点：有许多时间序列数据不是平稳的，或者顶多只是近似平稳的，并且也有检验平稳性的方法，那么，为什么非平稳时间序列在实践中用的不多？

他提供了四个原因：1. 对多样性的恐惧：平稳时间序列有唯一的模型 (Fourier-Cramer 模型)，而非平稳时间序列可以很复杂，并且会有多种多样的模型，令人生畏；2. 教育：许多本科时间序列课程只有时间和勇气教平稳时间序列；3. 数学上的方便：数学上，平稳模型更容易研究，并且相应的渐进理论也更容易；4. 成熟度：平稳时间序列的理论很成熟且应用广泛。

作者然后强调，现实中，许多时间序列不是平稳的，而常常具有趋势性 (于是一阶平稳性不成立)，季节性，或者方差会变 (于是二阶平稳性不成立)。可以用某些方法把不平稳的时间序列变成平稳的，比如差分，变量变换比如求对数或者开根号等 (对于指数增长的时间序列，取对数可以让方差平稳，然后再取差分可以让均值平稳；对于 \(x^2\) 这样的序列开根号可以让方差平稳)。

二阶平稳性的检验

作者假定趋势性和季节性都已经去除了，然后要检验二阶平稳性。这里的“检验”，指的是严格意义上的统计假设检验。接下来讲了多种方法中的两种；之所以讲这两种是因为它们已经有 R 语言的实现了。

Priestley-Subba Rao (PSR) 检验

PSR 检验专注于随时间变化的傅立叶谱 \(f_t(w)\)，这里 \(t\) 是时间，\(w\) 是频率。对于平稳时间序列，时变谱自然是与时间无关的常数。PSR 检验的就是 \(f_t(w)\) “不是常数”的程度。它看的是 \(f_t(w)\) 的一个估计量的对数，即 \[ Y(t,w) = \log[F_t(w)], \] 这里 \(F_t(w)\) 是 \(f\) 的一个估计量。于是近似地有 \[ E[Y(t,w)] = \log[f_t(w)], \] 并且 \(Y(t,w)\) 的方差近似为常数。这里，取对数操作是为了让方差平稳，这让我们可以集中关注 \(Y\) 的均值的变化。于是我们可以把 \(Y(t,w)\) 写成具有常数方差的线性模型，然后用标准的 ANOVA (analysis of variance) 方法检验 \(f\) 是否为常数。

接下来作者讲了基于 R 的示例，使用了地震数据。作者画出了时间序列的图，很明显方差是变化的，而统计检验的结果也证明了这一点。我照着作者的示例用 R 做了一下：

$ r

# 需要的包没有默认安装，所以需要先安装
> install.packages("fractal")
> install.packages("astsa")

# 载入包和数据
> library("fractal")
> library("astsa")
> data("eqexp")

# 画图
> exP <- eqexp[1:1024, 14]
> ts.plot(exP)

# PSQ 检验
> stationarity(exP)

# 最后的输出
Priestley-Subba Rao stationarity Test for exP
---------------------------------------------
Samples used              : 1024
Samples available         : 1020
Sampling interval         : 1
SDF estimator             : Multitaper
  Number of (sine) tapers : 5
  Centered                : TRUE
  Recentered              : FALSE
Number of blocks          : 10
Block size                : 102
Number of blocks          : 10
p-value for T             : 0
p-value for I+R           : 0.0003388896
p-value for T+I+R         : 0

p-value for T 这个参数等于零表明有强烈额证据拒绝“此时间序列是平稳的”这个零假设。

Block size 这个参数也有意思。作者没有明确说，但是对于时变频谱，肯定需要选取一个窗口大小，然后对这个窗口内的数据点做傅立叶变换。不大清楚这个大小怎么选出来的。

SDF estimator 是在估计功率谱密度。

小波频谱检验

这个方法是看一个叫做 \(\beta_j(t)\) 的统计量，这个量是局部平稳小波过程的小波频谱的一个线性变换 (Nason, von Sachs and Kroisandt, 2000)。需要看 \(\beta_j(t)\) (的估计量) 是否随时间变化。方法是看 \(\beta_j(t)\) 的估计量的 Haar 小波系数 (von Sachs and Neumann, 2000)。一个函数当且仅当其所有 Haar 小波系数为 0 时为常数，所以需要对 Haar 小波系数 (可能随时间变化) 进行多重统计检验。作者提到这种方法还有一些后续发展。

为了使用这种方法，需要安装相当大的一个 R 包，叫做locits。

> install.packages("locits")

> library("locits")

# 使用之前的数据进行检验
> ans <- hwtos2(exP)
> ans

# 画图
> plot(ans)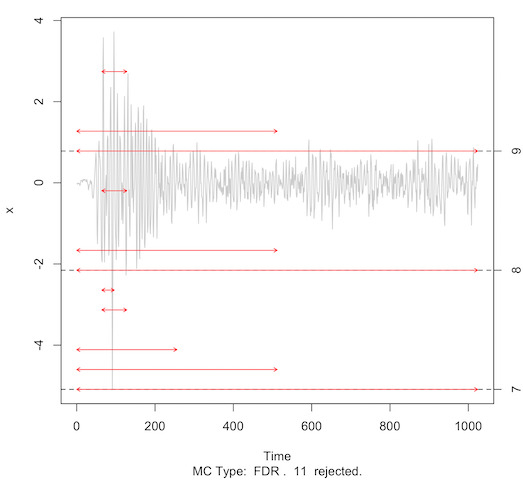

这种方法的一个优点是，可以定位出对平稳性的违背发生在什么地方，因为假设检验知道 Haar 小波系数的零假设不成立的尺度和地点。上图中的红色尖头给出了识别出的非平稳性，灰色线是时间序列本身。

其它检验平稳性的方法

待续